Unveiling the Power of Calculus
A Journey into Mathematical Analysis
Calculus is indeed a fundamental branch of mathematics that plays a crucial role in various fields, including physics, engineering, computer science, economics, and more. It provides a framework for understanding and analyzing change and motion, making it a powerful tool for solving real-world problems. There are two main branches of calculus: differential calculus and integral calculus. In essence, mathematical analysis is the systematic study of mathematical concepts, including those from calculus, using rigorous proofs and logical reasoning. It helps establish the validity of mathematical results and provides a deeper understanding of the underlying principles.
Overall, calculus and mathematical analysis together form a powerful set of tools that are indispensable in solving a wide range of mathematical problems and have numerous applications in various scientific and engineering disciplines.
What is Analysis?
Analysis is a meticulous study of mathematical entities, with a paramount focus on precisely and accurately unraveling their qualitative and quantitative behaviors. Real analysis stands as the theoretical bedrock supporting calculus, the very computational tool set employed to manipulate functions.
In this exploration, we will scrutinize familiar entities from introductory calculus—numbers, sequences, series, limits, functions, definite integrals, derivatives, and more. While you possess considerable experience in computing with these objects, our focus will pivot towards the intersection point of analysis and calculus. Here, we delve into the theoretical nuances that underpin these fundamental mathematical concepts, seeking to seamlessly weave together the computational prowess of calculus with the analytical depth of real analysis. The questions addressed will extend beyond mere computation, forming a rich tapestry that unites the practical and theoretical aspects of these intertwined mathematical disciplines.
Why Do Analysis?
It is a fair question to ask, “Why bother?”, when it comes to analysis. There is a certain philosophical satisfaction in knowing why things work, but a pragmatic person may argue that one only needs to know how things work to do real-life problems. The calculus training you receive in introductory classes is certainly adequate for you to begin solving many problems in physics, chemistry, biology, economics, computer science, finance, engineering, or whatever else you end up doing - and you can certainly use things like the chain rule, L’Hˆopital’s rule, or integration by parts without knowing why these rules work, or whether there are any exceptions to these rules. However, one can get into trouble if one applies rules without knowing where they came from and what the limits of their applicability are. Let me give some examples in which several of these familiar rules if applied blindly without knowledge of the underlying analysis, can lead to disaster.
Example 1.2.1(Division by Zero).
This is a very familiar one to you: the cancellation law \(ac = bc \implies a = b\) does not work when \(c = 0\). For instance, the identity \(1 \times 0 = 2 \times 0\) is true, but if one blindly cancels the \(0\) then one obtains \(1 = 2\), which is false. In this case, it was obvious that one was dividing by zero; but in other cases it can be more hidden.
Example 1.2.2(Divergent Series).
You have probably seen geometric series such as the infinite sum
\[S = 1 + \frac{1}{2}+ \frac{1}{4}+ \frac{1}{8} + \frac{1}{16} + \ldots\] You have probably seen the following trick to sum this series: if we call the above sum \(S\), then if we multiply both sides by \(2\), we obtain,
\[ 2S = 2+1+\frac{1}{2}+ \frac{1}{4}+ \frac{1}{8} +\ldots \ = 2+S \]
and hence \(S =2\), so the series sums to \(2\). However, if you apply the same trick to the series
\[S = 1+2+4+8+16+ \ldots\]one gets nonsensical results:
\[ 2S = 2+4+8+16+\ldots = S-1 \implies S = -1. \]
So the same reasoning that shows that \(\displaystyle 1+ \frac{1}{2}+ \frac{1}{4}+ \frac{1}{8}+ \ldots =2\) also gives that \(1 + 2 + 4 + 8 + . . . = −1\). Why is it that we trust the first equation but not the second? A similar example arises with the series
\[ S = 1 − 1 + 1 − 1 + 1 − 1 + . . . \]
we can write
\[ S = 1 − (1 − 1 + 1 − 1 + . . .) = 1 − S \]
and hence that \(S = 1/2\) or instead we can write
\[ S = (1 − 1) + (1 − 1) + (1 − 1) + . . . = 0 + 0 + . . . \]
and hence that \(S = 0\) or instead we can write
\[ S = 1 + (−1 + 1) + (−1 + 1) + . . . = 1 + 0 + 0 + . . . \]
and hence that \(S = 1\). Which one is correct?
Here we can question \(\displaystyle \sum_{n=1}^{ \infty}(-1)^n\) convergent or divergent? Also, How do you justify your answer?
So consider the series \(\displaystyle \Big((-1)^na\Big)_{n=0}^{\infty} \; a>0\) i.e., the series:
\[ \sum_{n=0}^{\infty} (-1)^n = \ (+a) +(-a) +(+a)+(-a)+ \ldots \infty \]
Easily by mathematical induction,
\[ s_n= \begin{cases} a & n\ge 0\\ -a & n\;\text{is odd} \end{cases} \]
then the sequence of partial sums is \((a,0,a,0,a,\ldots)\). Since this sequence is not convergent, the series is divergent.
So, the above implementation is for a general case you can take \(a=1\) then you’ll get it.
Also, we can take another problem. Here’s slight variation of the previous example.
Example(Divergent Sequence)
Let \(x\) be a real number, and let \(L\) be the limit. then
\[ \lim_{n \to \infty} x^n =L \]
Changing variables \(n=m+1\) we have,
\[ \lim_{m+1 \to \infty} x^{m+1} = \lim _{m+1 \to \infty} x \times x^m = x\; \lim_{m+1 \to \infty} x^m \]
But if \(m+1 \to \infty\), then \(m \to \infty\), thus
\[\lim_{m+1 \to \infty} x^m = \lim_{m \to \infty} x^m = \lim_{n \to \infty} x^n =L\] and thus,
\[ xL =L \]
At this point we could cancel the \(L’s\) and conclude that \(x = 1\) for an arbitrary real number \(x\), which is absurd. But since we are already aware of the division by zero problems, we could be a little smarter and conclude instead that either \(x = 1\), or \(L = 0\). In particular, we seem to have shown that
\[ \lim_{n \to \infty} x^n = 0\; \forall\ x\not=1 \]
But this conclusion is absurd if we apply it to certain values of \(x\), for instance by specializing to the case \(x = 2\) we could conclude that the sequence \(1, 2, 4, 8, . . .\) converges to zero, and by specializing to the case \(x = −1\) we conclude that the sequence \(1, −1, 1, −1, . . .\) also converges to zero. These conclusions appear to be absurd; what is the problem with the above argument?
Proposition: Let \(0<x<1\). Then we have \(\displaystyle \lim_{n\to \infty} x^n =0.\)
Example 1.2.3 (Interchanging integrals).
The interchanging of integrals is a trick which occurs just as commonly as integrating by sums in mathematics. Suppose one wants to compute the volume under a surface \(z = f(x, y)\) (let us ignore the limits of integration for the moment). One can do it by slicing parallel to the \(x-axis\): for each fixed value of \(y\), we can compute an area \(\int f(x, y) dx\), and then we integrate the area in the \(y\) variable to obtain the volume
\[ V=\int \int f(x,y)dxdy. \]
Or we could slice parallel to the \(y-axis\) to obtain an area \(\int f(x, y) dy\), and then integrate in the \(x-axis\) to obtain \[V=\int \int f(x,y)dydx.\]
This seems to suggest that one should always be able to swap integral signs:
\[\int \int f(x,y)dxdy = \int \int f(x,y)dydx.\] And indeed, people swap integral signs all the time, because sometimes one variable is easier to integrate in first than the other. However, just as infinite sums sometimes cannot be swapped, integrals are also sometimes dangerous to swap. An example is with the integrand \(e^{-xy}-xye^{-xy}\). Suppose we believe that we can swap the integrals:
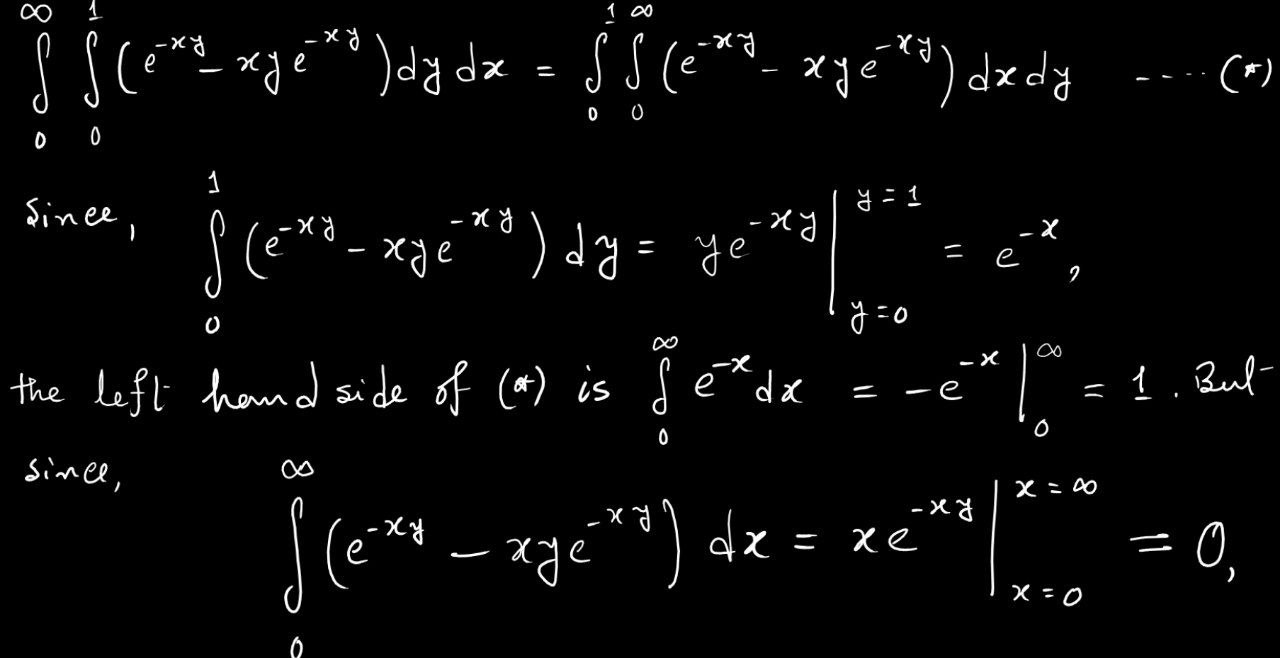
the right-hand side of \((*)\) is \(\int_{0}^{1} 0\ dx =0\) . Clearly \(1 \not= 0\), so there is an error somewhere but you won’t find one anywhere except in the step where we interchanged the integrals. So how do we know when to trust the interchange of integrals?
The analysis you learn will help you resolve these questions, and will let you know when these rules (and others) are justified, and when they are illegal, thus separating the useful applications of these rules from the nonsense. Thus they can prevent you from making mistakes, and can help you place these rules in a wider context. Moreover, as you learn analysis you will develop an “analytical way of thinking”, which will help you whenever you come into contact with any new rules of mathematics, or when dealing with situations which are not quite covered by the standard rules (e.g., what if your functions are complex-valued instead of real-valued? What if you are working on the sphere instead of the plane? What if your functions are not continuous, but are instead things like square waves and delta functions? What if your functions, or limits of integration, or limits of summation, are occasionally infinite?). You will develop a sense of why a rule in mathematics (e.g., the chain rule) works, how to adapt it to new situations, and what its limitations (if any) are; this will allow you to apply the mathematics you have already learnt more confidently and correctly.
Discovery of Calculus
Calculus was discovered in the middle of the \(1670\)’s which was a breakthrough in mathematics. The word comes from Latin meaning small stones because it deals with problems where big thing needs to be broken down into lots of little things. Without it, humans would never have left our own planet. Engineers use it to determine how much material they need for a job or how much power they should give a motor. Biologists use it to determine the rate of disease spread and chemists use it to measure reactions.
But where did this magical tool come from?
The earliest questions that calculus was invented to answer came in the form of paradoxes. We are going to understand and explore a paradox that will help us to explore the fundamental concept of calculus which is the backbone of mathematics.
Zeno: Achilles and the Tortoise
Zeno of Elea, an ancient Greek philosopher famous for inventing a number of paradoxes, arguments that seem logical, but whose conclusion is absurd or contradictory. For more than 2,000 years, Zeno’s mind-bending riddles have inspired mathematicians and philosophers to better understand the nature of infinity. He had a strange but interesting view of the world. He thought that we couldn’t trust our senses but only logic and invented a paradox to demonstrate one of the best-known problems are called the ’dichotomy paradox’, ‘Achilles and the Tortoise (disambiguation)’.
What the Tortoise Said to Achilles
“What the Tortoise Said to Achilles”, written by Lewis Carroll in 1895 for the philosophical journal Mind, is a brief allegorical dialogue on the foundations of logic. The title alludes to one of Zeno’s paradoxes of motion, in which Achilles could never overtake the tortoise in a race. In Carroll’s dialogue, the tortoise challenges Achilles to use the force of logic to make him accept the conclusion of a simple deductive argument. Ultimately, Achilles fails, because the clever tortoise leads him into an infinite regression.
Read the Summary of the dialogue from a Wikipedia source.
Zeno of Elea (c. 495 – c. 430 BC) did not advance any views concerning the infinite. Nevertheless, his paradoxes, especially “Achilles and the Tortoise”, were important contributions in that they made clear the inadequacy of popular conceptions. The paradoxes were described by Bertrand Russell as “immeasurably subtle and profound”. Achilles races a tortoise, giving the latter a head start.
Step 1: Achilles runs to the tortoise’s starting point while the tortoise walks forward.
Step 2: Achilles advances to where the tortoise was at the end of Step 1 while the tortoise goes yet further.
Step 3: Achilles advances to where the tortoise was at the end of Step 2 while the tortoise goes yet further.
Step 4: Achilles advances to where the tortoise was at the end of Step 3 while the tortoise goes yet further.
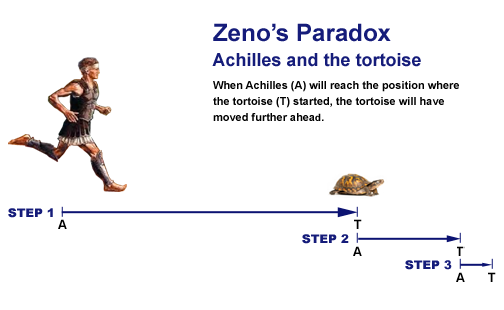
Apparently, Achilles never overtakes the tortoise, since however many steps he completes, the tortoise remains ahead of him.
Zeno was not attempting to make a point about infinity. As a member of the Eleatics school which regarded motion as an illusion, he saw it as a mistake to suppose that Achilles could run at all. Subsequent thinkers, finding this solution unacceptable, struggled for over two millennia to find other weaknesses in the argument.
Finally, in 1821, Augustin-Louis Cauchy provided both a satisfactory definition of a limit and a proof that, for \(0 < x < 1\),
\[ a+ax+ax^2+ax^3+ \ldots = \frac{a}{1-x}\;\; \text{when}\;|x| <1 \]
Suppose that Achilles is running at 10 meters per second, the tortoise is walking at 0.1 meters per second, and the latter has a 100-meter head start. The duration of the chase fits Cauchy’s pattern with a = 10 seconds and x = 0.01. Achilles does overtake the tortoise; it takes him
\[ 10+0.1+0.001+0.00001+\ldots = \frac{10}{1-0.01} = \frac{10}{0.99} = 10.10101\ldots seconds \]
Achilles will always be catching up to the place the tortoise was as the tortoise inches forward. The gap will get smaller, but the tortoise is always slightly ahead. According to Greek philosopher Zeno of Elea, who dreamed up this paradox 2500 years ago, the fastest runner in the world can never overtake a tortoise in a race because you infinitely divide the distance between them as the tortoise advances. But that’s ridiculous. We know it’s not true. Even with the head start, you could outrun a tortoise and you aren’t Achilles. So how can this be a paradox?
Can Mathematics Conquer Achilles?
Zeno knew Achilles could catch up to the tortoise in real life, but couldn’t prove it mathematically. He thought there would be an infinite number of new points for the tortoise to reach that Achilles had to reach because he didn’t know that an infinite series of numbers could add up to a finite value. No one knew that for another 2000 years. Now we call a convergent series,
\[ \frac{1}{2}+ \frac{1}{4}+ \frac{1}{8} + \frac{1}{16} + \ldots \infty=1 \]
This infinite series goes on forever, but it eventually adds up to 1. And at that 1 is where, mathematically, Achilles finally reaches the tortoise. We knew that Achilles could catch up to the tortoise, but it took inventing calculus for us to prove why. This is why this paradox that confounded great minds for thousands of years is falsidical.
Dichotomy Paradox
Zeno’s Dichotomy Paradox involves a runner trying to reach a destination. According to Zeno, in order to reach the destination, the runner must first reach the halfway point. Once at the halfway point, the runner must then reach the new halfway point, and so on. The paradox argues that since there are an infinite number of halfway points to cover, the runner can never actually reach the destination because they would need to complete an infinite number of tasks in a finite amount of time.
The Dichotomy Paradox raises questions about the nature of infinity and the divisibility of space and time. It was one of Zeno’s attempts to illustrate the apparent absurdities and paradoxes that arise when one tries to analyze motion and change using the concept of infinity. However, it’s worth noting that Zeno’s paradoxes sparked important discussions in the history of philosophy and mathematics, and various solutions and interpretations have been proposed over the centuries.
Deducing Using Mathematics
Suppose a runner wants to travel a distance of 1 unit. According to Zeno, before reaching the destination, the runner must first reach the midpoint (0.5 units). Then, before reaching the destination from the midpoint, the runner must reach the new midpoint (0.75 units), and so on. This process continues indefinitely.
Mathematically, we can express the distance covered at each step as a geometric series. Let \(S\) represent the total distance covered, and each step as \(S_n\), where \(n\) is the number of steps:
\[ S = S_1+S_2+S_3+\ldots \]
At each step, the runner covers half of the remaining distance. So, \(S_n\) can be expressed as:
\[ S_n=1-\frac{1}{2^n} \]
And if you’re interested, the derivation is given below.
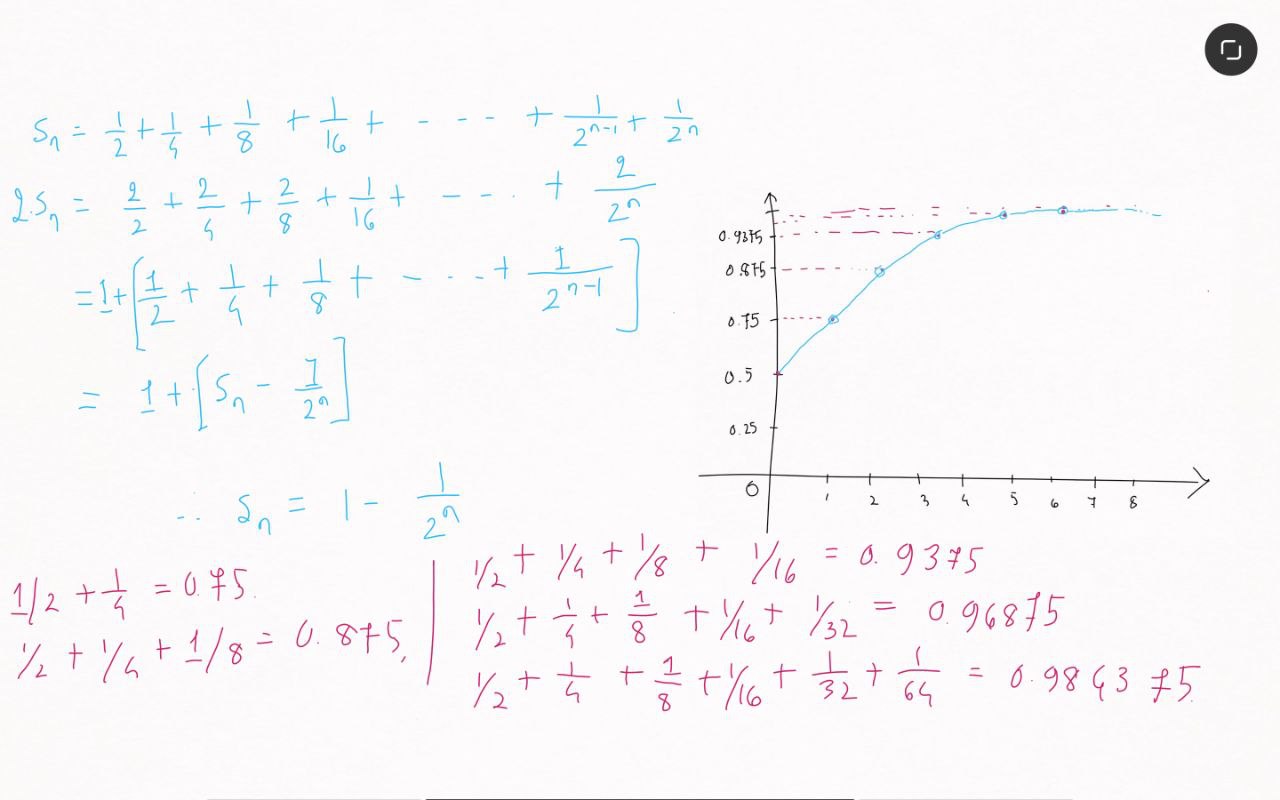
The total distance covered, \(S\), is the sum of all these steps:
\[ S=\frac{1}{2}+ \frac{1}{4}+ \frac{1}{8} + \frac{1}{16} + \ldots \infty \]
This is a geometric series that converges to 1. Therefore, according to the mathematical analysis, the runner will cover the entire distance, and the sum of the infinite series will be finite (1 unit).
The resolution of Zeno’s Dichotomy Paradox lies in the fact that although there are infinitely many steps, the sum of the series converges to a finite value, allowing the runner to reach the destination. This reconciliation involves concepts from calculus, particularly the idea of an infinite sum converging to a finite value.
Conclusion
Calculus provides the tools to precisely define and calculate limits, analyze infinite series, and understand the behavior of functions as they approach certain values or extend to infinity. The reconciliation of Zeno’s paradox through the convergence of an infinite series is a demonstration of how mathematical concepts, particularly those in calculus, can be used to address seemingly paradoxical situations involving infinity and motion. This is just one example of how calculus helps us understand and model dynamic processes in the real world.
In Zeno’s Dichotomy Paradox, the use of geometric series, limits, and convergence illustrates how calculus helps make sense of infinite processes, showing that even though there are infinitely many steps, a finite result can be achieved.
Similarly, in Achilles and the Tortoise, the concept of infinite series, along with the understanding of limits and convergence, demonstrates how calculus resolves the paradox, allowing Achilles to overtake the Tortoise despite an infinite number of steps.
These paradoxes highlight the historical intersection of philosophy and mathematics, showcasing the significance of calculus in addressing complex questions related to motion, continuity, and infinity. They serve as early examples of how mathematical thinking evolved to provide solutions to seemingly paradoxical scenarios, laying the groundwork for further developments in the understanding of dynamic processes.
See Also
References
